AGC005C Tree Restoring 题解 (构造+结论)

作者：XiaoQuQu，发表于 Wed Feb 28 2024。

哎呀小清新题。

题意

给定长度为 $n$ 的数组 $a$，求是否存在 $n$ 个节点的一棵树满足节点 $i$ 到他的最远节点的距离为 $a_i$。

题解

设 $mx=\max a_i,mn=\min a_i$，$c_i$ 表示数字 $i$ 在数组 $a$ 中的出现次数。

由经典结论：树上离一个点最远的点必定是直径的一个端点可得，$i$ 离一个直径端点的距离是 $a_i$，所以我们可以把这些点分为两类：一类的 $a_i$ 是由第一个端点贡献的，另一类的 $a_i$ 由第二个端点贡献。

然后我们可以先把这个直径给构造出来，考虑到我们需要构成一条直径，所以必定要有 $\forall i \in (mn,mx],c_i\ge2$。

发现如果当 $mx$ 是奇数，说明我们的直径上有偶数个点，于是 $c_{mn}=2$，否则如果 $mx$ 是奇数，$c_{mn}=1$。

然后如果此时你写一下这个东西发现过了，接下来我们证明以上两个条件的充分性，也就是尝试构造一个树满足题意。

在这里我们讨论 $mx$ 是奇数的情况，偶数同理。

由于 $\forall i\in (mn,mx],c_i\ge2$，我们可以先构造出这个直径，并将直径上半边的点标上号（下图中由于位置不够用 $p$ 代替 $mx$，$q$ 代替 $mn$）：

接下来，对于所有 $i$，如果 $c_i>2$，就说明还有 $c_i-2$ 个点没有被我们考虑到，于是我们可以将这些点挂到标号为 $i-1$ 的点上。

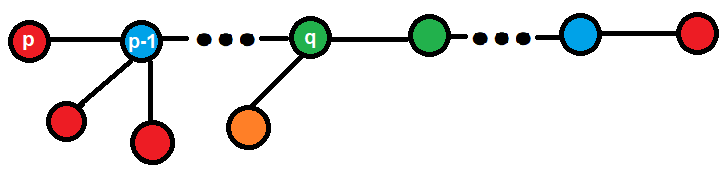
显然被挂上去的点距离另外半边的直径端点距离为 $i$，于是我们就完成了构造。实际实现的时候注意特判一下 $1$。

const int MAXN = 105;
int n, cnt[MAXN], a[MAXN];

void work() {
	cin >> n;
	for (int i = 1; i <= n; ++i) cin >> a[i];
	for (int i = 1; i <= n; ++i) cnt[a[i]]++;
	int mx = *max_element(a + 1, a + 1 + n), mn = *min_element(a + 1, a + 1 + n);
	if (cnt[1]) {
		if (n == 2) return puts("Possible"), void();
		if (cnt[1] > 1 || mx != 2) return puts("Impossible"), void();
		puts("Possible");
		return;
	}
	for (int i = mx; i >= mn; --i) {
		if (cnt[i] <= 1 && i != mn) return puts("Impossible"), void();
	}
	if (cnt[mn] > 2) return puts("Impossible"), void();
	if (((mx & 1) && (cnt[mn] == 1)) || (!(mx & 1) && (cnt[mn] == 2)))
		return puts("Impossible"), void();
	puts("Possible");
}